Una de las herramientas básicas que conocer para construir geometría creo que es la papiroflexia, principalmente con los origamis que nos permiten crear estructuras realmente consistentes con simple papel.
Este fractal lo he construido con alumnos y alumnas de 4º de E.S.O. durante una semana cultural en el Instituto. Los materiales necesarios son:
- Papel (reciclado, tanto del alumnado como del centro)
- Paciencia :-)
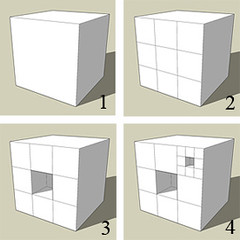
La base para construir los cubos que forman la esponja de Menger es una forma que se llama módulo sonobe, es más fácil ver una imagen de cómo se hacen:
El módulo sonobe es la última figura de la imagen. Para hacer la esponja (que se ve al final de este post) hacen falta unos 800 módulos sonobe... así que es mejor enseñarles a principio de curso, y cuando han terminado pronto ejercicios de clase, cuando tienen una hora de guardia, cuando están aburridos en el recreo... van haciendo figuras y entregándolas... y para abril tendremos suficientes (cuando aprenden las hacen con una habilidad tremenda y les "pica" ponerse a hacer).
Con estos módulos sonobe se construyen cubos, doblando por las líneas de puntos que se ven en la imagen, metiendo las solapas de unos módulos sonobe dentro de otros, la forma más fácil de aprender es viendo un vídeo, comó éste:
Y uniendo cubos y cubos... formamos el cubo que se ve en la siguiente imagen. Fijáos en que hay un alumno de 4º apoyado... ¿veis la resistencia que tiene?:
La visión espacial que crea esta figura es asombrosa, y se puede practicar, por ejemplo, la fórmula de Euler. Además el trabajar con módulos sonobe fomenta mucho la imaginación, porque el mismo alumnado creaba estructuras por su cuenta :-)
La primera imagen y más información sobre la esponja de Menger se puede encontrar en el estupendo blog Juegos Topológicos.